How many radicals do you need to write an (algebraic) number?
While learning Galois theory, I had an intuition about the relationship between the number of radicals you need to nest to write an algebraic number exactly, and the number of groups in the abelian chain connecting the Galois group to the trivial group. After searching for a few minutes and not finding a proof, I decided to attempt one myself. The image serves to help illustrate the proof.
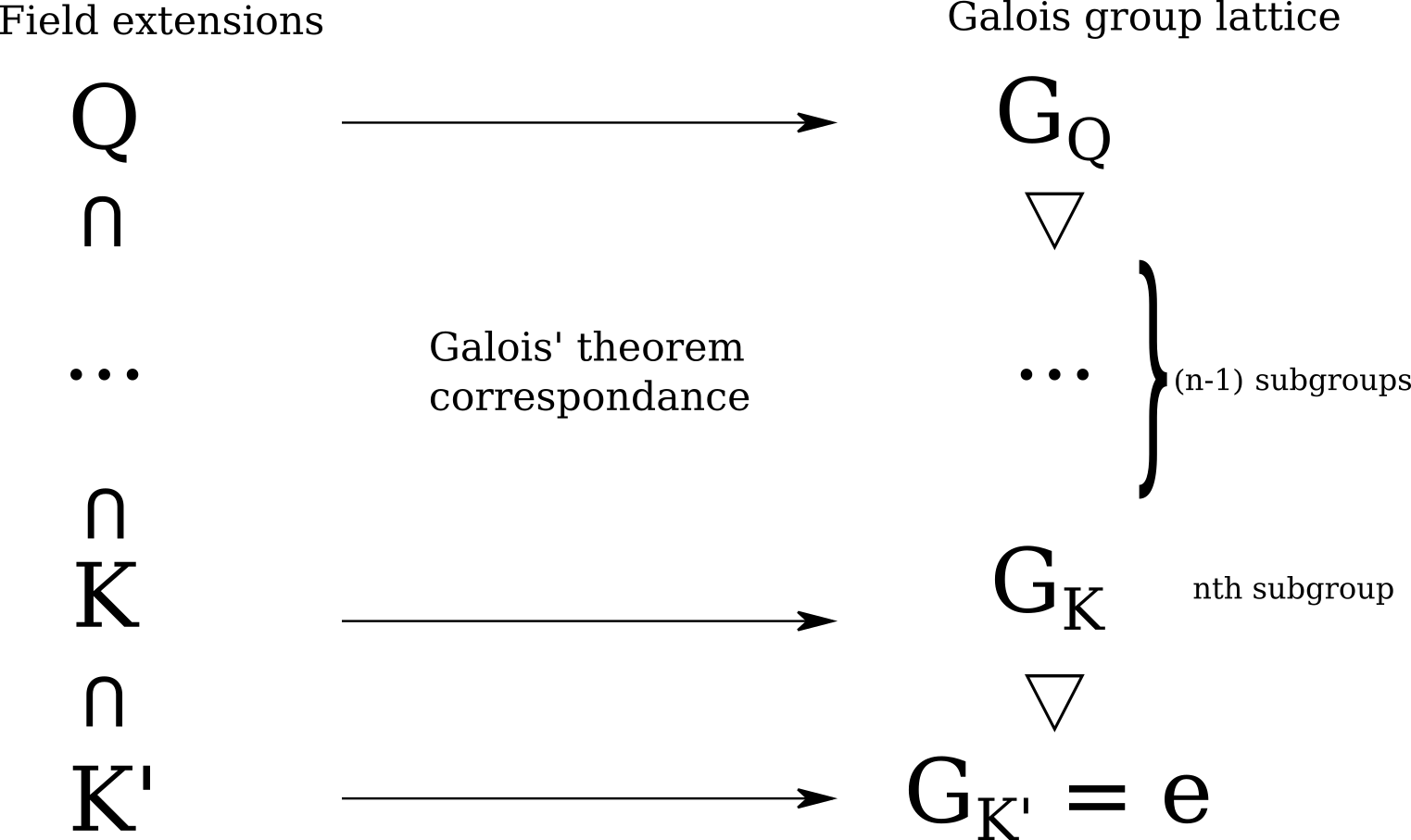
Theorem: If $\alpha$ is an algebraic number, then the minimum number of radicals required to represent $\alpha$ is equal to the number of subgroups in the abelian tower of the galois group of $\alpha$’s minimal polynomial.
Proof (by induction):
For the base case, we let $n=0$, i.e. $\alpha$ takes 0 radicals to write, which means that $\alpha \in \mathbb{Q}$. Then the minimal polynomial is $x - \alpha = 0$, which has $\alpha$ as a root, and the Galois group is trivial. Then the number of subgroups in the Abelian tower is zero.
For the inductive step, let $\alpha$ be an algebraic number which takes $n$ radicals to write. Then we can write \(\alpha = a (\beta)^{1/k} + b\) for some $\beta$ which takes $n-1$ many radicals to write. Suppose by our hypothesis that the Galois group of $\beta$’s minimal polynomial $m_\beta (x)$ has $n-1$ many subgroups in it’s Abelian tower. We want to show that $\alpha$ has $n$ many subgroups in it’s Abelian tower.
Let $K$ be the splitting field of $m_\beta (x)$. We can construct the minimal polynomial $m_\alpha (x)$ of $\alpha$ over $K$ as $(\frac{\alpha - b}{a})^k = 0$, and then construct the splitting field $K’$ of $\alpha$ in $K$. Since $\alpha$ is constructable, the Galois group $G_{K’}$ of $K’$ must have an abelian tower, and since each solvable Galois group has only one tower, we know that the tower of length $n-1$ for $\beta$ in $G_K$ is included as a subset if $G_K$ is a normal subgroup of $G_{K’}$. Thus if we can prove that $G_{K’} \trianglelefteq G_{K}$, that will be the $n$th group in the Abelian tower, and we will be done. However, $K’$ was the splitting field of $m_\alpha (x)$ over $K$, and hence is a normal extension of $K$. By the fundamental theorem of Galois theory, this means that $G_{K’}$ is a normal subgroup of $G_{K}$ as required.
Then the result follows from the principle of mathematical induction.